TERCER PARCIAL

GEOMETRÍA ANALÍTICA

Propósito de la asignatura:
Que el estudiante interprete, argumente, comunique y resuelva diversas situaciones pro-blemáticas de su contexto por medios gráficos y analíticos, que incluyan la representación de figuras en el plano cartesiano.

Relación de la materia con otras asignaturas:
*Lectura, Expresión Oral y Escrita: Comprensión y escritura de textos, comunicación y argumentación de ideas o soluciones de situaciones problemáticas.
*Química: Construcción de modelos matemáticos y en la solución de los modelos que resulten de estas formulaciones, graficación de átomos y moléculas en el plano o en el espacio.
*Inglés: Traducción y comprensión de textos en una segunda lengua que se requieran utilizar en la solución de problemas matemáticos de la vida cotidiana.
*CTSyV: Construcción de modelos matemáticos que representen el desarrollo sustentable, deterio-ros y/o hechos sociales.
*TIC: Empleo de herramientas computacionales para facilitar el aprendizaje de las Matemáticas.
*Biología y Ecología: Aplicar modelos matemáticos para interpretar procesos biológicos y ecológicos.
*Física: Uso de modelos matemáticos, representación gráfica de los fenómenos naturales, conver-siones de unidades, etc.
*Dibujo Técnico: Graficación de figuras geométricas, líneas, acotaciones, ángulos, etc.

Competencias propuestas para desarrollar en el estudiante:

1. Construye e interpreta modelos matemáticos mediante la aplicación de procedimientos aritméticos, geométricos y variacionales, para la comprensión y análisis de situaciones reales, hipotéticas o formales.
2. Formula y resuelve problemas matemáticos, aplicando diferentes enfoques.
3. Explica e interpreta los resultados obtenidos mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales.
4. Argumenta la solución obtenida de un problema con métodos numéricos, gráficos, analíticos o variacionales, mediante lenguaje verbal, matemático y el uso de las tecnologías de la información y la comunicación.
5. Analiza las relaciones entre dos o más variables de un proceso social o natural para determinar o estimar su comportamiento.
6. Cuantifica, representa y contrasta experimental o matemáticamente las magnitudes del espacio y las propiedades físicas de los objetos que lo rodean.
7. Elige un enfoque determinista o uno aleatorio para el estudio de un proceso o fenómeno, y argumenta su pertinencia.
8. Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científicos.

Estructura conceptual de la materia:

Historia de la Geometría Analítica:
*Los egipcios desarrollaron los denominados Papiro de Ahmes y Papiro de Moscú muestran conjuntos de métodos prácticos para obtener diversas áreas y volúmenes.

*Euclides, sintetiza en su obra cumbre, Los elementos, modelo de sistema axiomático-deductivo. Sobre tan sólo cinco postulados y las definiciones que precisa construye toda la Geometría y la Aritmética conocidas hasta el momento.
*Arquímedes analizó exhaustivamente las secciones cónicas, e introdujo en geometría otras curvas como la espiral .

*Apolonio trabajó en varias construcciones de tangencias entre círculos, así como en secciones cónicas y otras curvas.
*Se publica por primera vez como "Geometría analítica", apéndice al Discurso del método, de Descartes(1637).

*Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes.
*Omar Khayyam  en el siglo XI utilizo un método muy parecido para determinar ciertas intersecciones entre curvas, es imposible que alguno de los citados matemáticos franceses tuvieran acceso a su obra.
*La aparición de la geometría analítica corrió parejo a la de la geometría cartesiana, y ambas son indistinguibles.
*La geometría analítica comprende no sólo a la geometría cartesiana, sino que se basa en la construcción de ejes coordenados y la descripción de las figuras mediante funciones, algebraicas o no.
*Gauss devuelve el carácter geométrico que impregna parte del análisis matemático, fundamentalmente con dos contribuciones: el nacimiento del análisis complejo y de la geometría diferencial. Marcando con ello el fin de la geometría analítica como disciplina.

*Con el desarrollo de la geometría algebraica, se puede certificar totalmente la superación de la geometría analítica.

PROGRAMA PARA LA ASIGNATURA DE GEOMETRIA ANALITICA

1.-COORDENADAS RECTANGULARES

Sistemas Coordenados

Segmentos dirigidos

Distancia entre dos puntos

División de un segmento dada una razón

2.-COORDENADAS POLARES

Radio vector

Angulo polar

Transformación a coordenadas rectangulares y viceversa

3.- LUGARES GEOMETRICOS

Áreas y perímetro

Simetría

Asíntota

4.- LA RECTA

Pendiente y ángulo de inclinación

Intersección de rectas

Ecuaciones

5.-SECCIONES CONICAS

Circunferencia

Parábola

Elipse

COORDENADAS RECTANGULARES

Sistemas Coordenados
    
a)      Unidimensional
Es la relación de números y letras

b) Bidimensional

Relación entre una letra mayúscula con dos números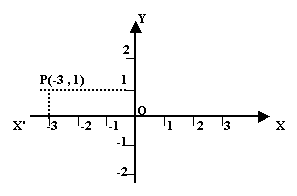

c) Tridimensional
Establece correspondencia entre puntos en el espacio mediante tres coordenados X,Y ,z y un        punto origen, permite definir ecuaciones en X,Y,Z que representan superficies como la esfera

Segmentos dirigidos

Es un segmento d erecta que tiene dirección. Es decir que tiene un extremo inicial y otro que es final. Los segmentos se denotan igual a los segmentos pero se respeta su dirección.

Ejemplo: en la notación AB, A es el punto inicial y B el punto final. De esta manera BA es otro segmento dirigido con dirección opuesta.

Distancia entre dos puntos

Primeramente definamos la diferencia entre distancia y longitud

Longitud: La longitud es una magnitud creada para medir la distancia entre dos puntos y conocer su altura.

Distancia: Expresa la proximidad  o lejanía entre dos objetos el «camino más corto» entre dos puntos es un segmento recto con curvatura llamada geodésica.

La formula para calcular la distancia entre dos puntos

 

Recordemos que no existen distancias negativas por lo tanto siempre obtendremos el valor absoluto

Ejercicios

1. Halla la distancia entre A y B en cada caso:
    a. A(-7, 4), B(6, 4)      b. A(3, 4), B(3, 9)      c. A(-5, 11), B(0, -1)
2. Calcula el valor de k para que la distancia de A(-1, 4) a B(k, 1) sea igual a 5.
3. Halla las coordenadas de dos puntos tales que la distancia entre ellos sea igual a 4.
4. Calcula el perímetro de los siguientes triángulos y clasifícalos según la longitud de sus lados:    a. A(-2, 2), B(1, 6), C(6, -6)      b. A(-5, -2), B(0, 6), C(5, -2)

División de un segmento dada una razón

Si un segmento se divide en n partes iguales, la razón para determinar las coordenadas de cada punto que divide a dicho segmento se calcula de la siguiente manera:

R es la razón de división del segmento

Para calcular la razón de división de un segmento realizamos lo siguiente. Si el segmento AB se divide en tres parte iguales la razón por cada punto es:

 

Las coordenadas para P1:

La razón es de ½  debido a que del punto A al punto P1 recorremos un espacio y del punto P1 a b recorremos dos espacios.

Por tal motivo la razón

Es  de 2/1 debido a que de A a P2 recorremos dos espacios y de P2 a B recorreos un espacio

Criterios de aplicación

1)      La razón es diferente debido a que  o es lo mismo  que  por que el segmento lleva distinta dirección

2)      Si el punto de división se encuentra dentro del segmento a dividir este tendrá signo positivo

                                                                                                                 

3)      Si el punto de división se encuentra fuera del segmento a dividir este tendrá signo  negativo

Esto se debe a que de A a P recorremos un espacio, pero es -2 debido a que de P a B nos regresamos recorriendo dos espacios.

El punto medio de un segmento de recta es igual a la razón 1/1.

Ejercicio: Encuentra la relación de los siguientes segmentos

COORDENADAS POLARES

En un sistema de coordenadas polares, un punto se localiza especificando su posición relativa respecto a una recta fija denominada eje polar y un punto fijo de ella conocido como polo (O). El polo se considera el origen del sistema de coordenadas, en donde el radio vector (r)  toma el valor de cero, el ángulo polar (Ө), el de 0°. En realidad, tal ángulo es indefinido, puesto que si el sistema gira, el ángulo varía constantemente. El origen del sistema está en (0,0°).

Los elementos básicos del sistema de coordenadas polares son:

·         El punto O se denomina polo

·         La semirrecta horizontal con extremo en el polo es el eje polar

·         P es un punto cualquiera del sistema de coordenadas

·         El segmento OP se denomina radio vector y se simboliza con r

·         El ángulo que forman el eje polar y el radio vector se denomina ángulo polar o ángulo vectorial y su símbolo es Ө

La posición del punto P respecto al eje polar y el polo se determina en base al radio vector y al ángulo polar estas dos cantidades son las coordenadas polares del punto P y simboliza como P(r,Ө).

Radio vector

El radio vector es la magnitud o distancia del segmento limitado en dos de sus extremos por el polo y un punto en específico del sistema de coordenadas polares. Se considera positivo cuando se mide desde el polo hacia el punto P y negativo cuando se mide desde el punto P al polo.

Angulo Polar

El ángulo polar Ө se mide teniendo el eje polar como lado inicial y el radio vector como final, es decir se mide en sentido contrario al giro de las manecillas del reloj para que sea positivo; sin embargo es posible medirlo en sentido contrario y obtener un ángulo negativo.

Un par de coordenadas polares (r,Ө) determinan uno solamente un punto en el sistema de coordenadas polares; por el contrario un punto P que ha sido especificado por las coordenadas (r,Ө) corresponde a cualquier par de coordenadas representadas por  (r,Ө + 2∏n) en donde ∏ está dado en radianes y n es un numero entero cualquiera; la razón de esto es cada vuelta corresponde a 2∏ radianes.  El ángulo polar puede expresarse en radiaciones, aunque es más común expresarlo en grados sexagesimales.

Equivalencias:

Para localizar un punto cualquiera en el plano polar, el procedimiento consiste en situarse en el polo, ubicar la línea que contenga el ángulo Ө y desplazarse sobre ella tantas unidades como lo especifique el radio vector.

Pr ejemplo para situar en el plano polar el punto P₁(3,30°), nos situamos en el polo, ubicamos la línea de 30° y nos desplazamos sobre ella tres unidades.

Transformación a coordenadas rectangulares y viceversa

Para transformar coordenadas polares a rectangulares y viceversa, es conveniente hacer coincidir al eje polar con la parte positiva del eje x y el polo con el origen cartesiano.

Las coordenadas de P son (x,y) en el sistema rectangular y (r,Ө) en el sistema polar. Observemos que en  la figura se forma un triángulo rectángulo, en el que la hipotenusa corresponde a r y los catetos a x y y. Si  consideramos ángulo Ө de ese triángulo , podemos establecer las siguientes relaciones trigonométricas:

Con base en estas equivalencias es posible hacer la transformación de coordenadas polares a rectangulares y viceversa.

Ejemplo de transformación es:

Analogía entre los sistemas coordenados

Coordenadas rectangulares	Coordenadas  polares
Su origen esta en el punto (0,0)	Su origen esta en el punto (0,0°)
Un punto cualquiera se localiza haciendo referencia a los ejes x y y	Un punto cualquiera se localiza haciendo referencia al radio vector y al angulo polar
Las coordenadas de cualquier punto se representa con el par ordenado (x,y)	Las coordenadas de cualquier punto se representa con el par ordenado (r,Ө)
Por convención, el eje x es una línea horizontal	Por convención, el eje polar es una línea horizontal

LUGARES GEOMETRICOS

Un lugar geométrico es un conjunto de puntos que satisfacen determinadas condiciones o propiedades geométricas.

En el plano

Ejemplos de lugares geométricos en el plano:
El lugar geométrico de los puntos que equidistan a otros dos puntos fijos A y B es una recta o eje de simetría de dichos dos puntos. Si los dos puntos son los dos extremos de un segmento {AB}, dicha recta o lugar geométricos, es llamada mediatriz y es la recta que se interseca perpendicularmente a {AB} en su punto medio.

La bisectriz es también un lugar geométrico. Dado un ángulo la bisectriz cumple la propiedad de que todos sus puntos equidistan a los lados de dicho ángulo, convirtiéndose la bisectriz en un caso particular del lugar geométrico que sigue a continuación.

Generalizando la propiedad de equidistancia a dos rectas, obtenemos que la paralela media es el lugar geométrico de los puntos que las equidistan. Se observa que, bajo el punto de vista de que las rectas paralelas se cortan en el infinito -se elimina, pues, la noción de paralelismo-, pasa a ser un sinónimo de la bisectriz, donde el ángulo ha tomado valor nulo. Si, por el contrario, se diferencia el concepto de paralelismo, la bisectriz vuelve a ser, como se ha dicho antes, un caso particular de esta definición y el caso de rectas paralelas, con ángulo 0, es disjunto al de las bisectrices (ángulo no nulo).

Secciones cónicas

Las secciones cónicas pueden ser descritas mediante sus lugares de geométria:

La circunferencia es el lugar geométrico de los puntos cuya distancia a un punto determinado, el centro, es un valor dado (el radio).
La elipse es el lugar geométrico de los puntos tales que la suma de su distancia a dos puntos fijos, los focos, es una constante dada (equivalente a la longitud del semieje mayor de la elipse).


La parábola es el lugar geométrico de los puntos cuya distancia a un foco equivale a su distancia a una recta llamada directriz.
La hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia entre sus distancias a dos puntos fijos, los focos, es igual a una constante (positiva), que equivale a la distancia entre los vértices.

 En el espacio

Figuras geométricas muy complejas pueden ser descritas mediante el lugar geométrico generado por los ceros de una función o de un polinomio. Por ejemplo, las cuádricas están definidas como el lugar geométrico de los ceros de polinomios cuadráticos.
En general, los lugares geométricos generados por los ceros del conjunto de polinomios reciben el nombre de variedad algebraica, las propiedades de dichas variedades se estudian en la geometría algebraica.

Áreas y perímetros

El perímetro y el área son magnitudes fundamentales en la determinación de un polígono o una figura geométrica; se utiliza para calcular la frontera de un objeto, tal como una valla. El área se utiliza cuando queremos obtener la superficie interior de un perímetro que se desea cubrir con algo, tal como césped o fertilizantes.

En el uso militar, el término perímetro define una área geográfica de importancia, como una instalación física o trabajo de la defensiva, pero también puede referirse a una estructura teórica como una defensa completa formada por un grupo pequeño de soldados, el propósito de que es protección mutua de nosotros en lugar de la defensa de territorio real.

Para conocer el perímetro de un polígono cualquiera debemos medir y sumar las longitudes de sus lados. Algunas figuras, debido a que tienen lados iguales, tienen fórmulas fáciles y rápidas con las que podemos calcular su perímetro.

Para obtener el perímetro de un polígono conociendo sus vértices basta con solo calcular las distancias entre ellos y sumarlas.

El área es una medida de la extensión de una superficie, expresada en unidades de medida denominadas superficiales. Para superficies planas el concepto es más intuitivo. Cualquier superficie plana de lados rectos puede triangularse y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).

Para calcular el perímetro de cualquier figura, utilizamos la fórmula de la distancia ya que el perímetro es la suma de todos las distancia.

Recordemos la fórmula de la distancia:

Por lo tanto la del perímetro es:

Perímetro= D₁ +D₂+D₃….

 Para calcular el área:

Rectas notables del Triangulo

En todo triangulo siempre es posible trazar cuatro rectas notables: mediana, altura, mediatriz y bisectriz, las cuales al intersecarse determinan los puntos notables del triángulo: baricentro, ortocentro, circuncentro e incentro, respectivamente.

MEDIANA

La mediana es el segmento trazado desde un vértice hasta el punto medio del la opuesto.

Como determinar los puntos medios de los lados del triangulo

Para determinar las ecuaciones de las medianas, debemos calcular el punto medio de cada uno de los tres lados del triángulo y luego aplicar la fórmula para determinar la ecuación de una recta cuando conocemos dos puntos por los que pasa.

1.- Puntos medios de los lados del triángulo.

2.- Determinación de la ecuación de cada mediana

Como determinar algebraicamente el baricentro

ALTURA

La altura de un triángulo es la perpendicular trazada desde un vértice al lado opuesto o a su prolongación.

Como determinar la ecuación de cada altura del triangulo

1.-Calculamos las pendientes de los tres lados del triángulo, aplicando la formula y las anotamos en el lado correspondiente:

2.-Deducimos sus recíprocos y les cambiamos de signo para obtener la pendiente de la perpendicular a cada lado.

3.- Tomamos las coordenadas del vértice opuesto de cada lado y la pendiente de la perpendicular respectiva. Con estos datos podemos determinar la ecuación de cada altura del triángulo, aplicando la formula punto pendiente.

Como determinar el ortocentro

Para determinar las coordenadas del ortocentro, es suficiente con resolver por cualquier método algebraico un sistema de ecuaciones simultaneas formado por las ecuaciones de dos alturas del triángulo.

Al resolver el sistema de ecuaciones correspondientes a las rectas hb y hc por el método de igualación, obtenemos:

MEDIATRIZ

La mediatriz es la perpendicular en el punto medio de cada triangulo. Como el triangulo tiene tres lados, hay tres mediatrices, las cuales se simbolizan con la letra M y un subíndice que corresponde a cada lado del triángulo.

El punto donde se intersecan las tres mediatrices se denomina circuncentro y corresponde al centro de una circunferencia que pasa por los tres vértices del triángulo.

Como determinar algebraicamente el circuncentro

Después de haber trazado las tres mediatrices y comprobando que su intersección ocurre en el centro de la circunferencia. A continuación se te muestra el proceso analítico para determinar las ecuaciones de las mediatrices y el circuncentro.

Ejemplo:

BISECTRIZ

La bisectriz de un ángulo es el lugar geométrico de los puntos equidistantes de los lados del ángulo; en otras palabras es la recta que divide a un ángulo en dos pates iguales.

Como determinar algebraicamente el incentro

El incentro es el punto de intersección de las bisectrices de un triángulo.

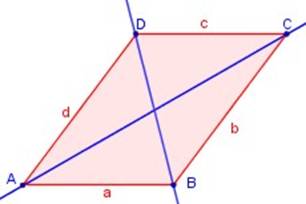
 Eje de simetría

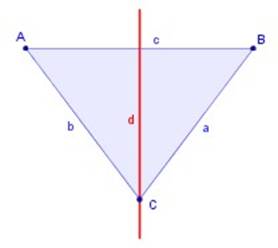
Eje de simetría es la línea que divide una figura en dos partes simétricas. En la figura a la derecha, la línea roja (d) que divide al triángulo ABC.

Otra definición para Simetría sería:  Proporción adecuada de las partes de un todo. Correspondencia de posición, forma y dimensiones de las partes de un cuerpo o una figura a uno y otro lado de un plano transversal (bilateral) o alrededor de un punto o un eje (radial).

También sabremos que  una figura es simétrica cuando podemos pasar una línea recta o eje por ella de tal forma que dicha línea divide la figura en dos partes que tienen la misma forma.

Por el contrario, una figura no es simétrica cuando, al trazar una línea recta por su mitad, la figura se divide en dos partes que tienen formas distintas.

Simetría en figuras planas

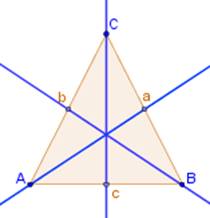	El triángulo equilátero tiene tres ejes de simetría.
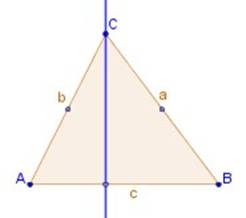	El triángulo isósceles tiene un solo eje de simetría.
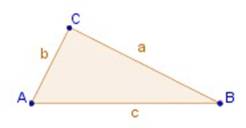	El triángulo escaleno no tiene ejes de simetría. Estas figuras sin ejes de simetría se llaman figuras asimétricas.
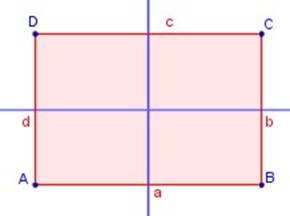	El rectángulo tiene dos ejes de simetría.
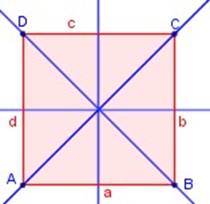	El cuadrado tiene cuatro ejes de simetría.
	El rombo tiene dos ejes de simetría.
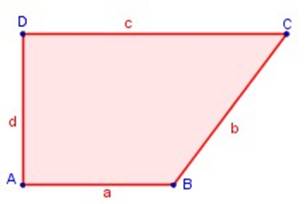	El trapecio no tiene ejes de simetría.
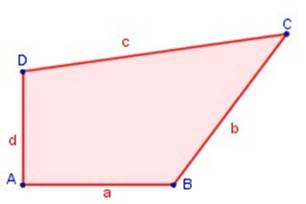	El trapezoide no tiene ejes de simetría.

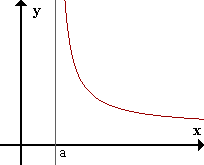
Asíntotas

Se llama asíntota de una función f(x) a una recta t cuya distancia a la curva tiende a cero, cuando x tiende a infinito o bien x tiende a un punto a.

Asíntota vertical

La recta x=a es asíntota vertical (AV) de f(x) si lim_x->a+ f(x) = inf o lim_x->a- f(x) = inf.

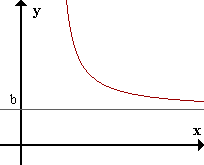
Asíntota horizontal

La recta y=b es asíntota horizontal (AH) de f(x) si lim_x->inf f(x) = b.

Ejemplo

f(x) = x/(x-1) limx->1+ f(x) = +inf limx->1- f(x) = -inf => x=1 es AV de f(x) limx->inf f(x) = 1 => y=1 es AH de f(x)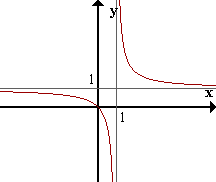

Definición

Asíntota oblicua

La recta y = mx + n es asíntota oblicua (AO) de f(x) si lim_x->inf f(x) - (mx + n) = 0.

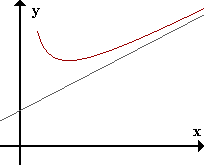
Ejemplo

f(x) = x + 1/x limx->inf f(x) - x = limx->inf x + 1/x - x = 0 => y=x es AO de f(x) Además, limx->0+ f(x) = +inf limx->0- f(x) = -inf => x=0 es AV de f(x)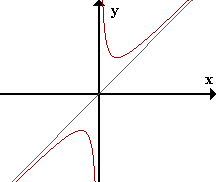

Teorema

y = mx + n es asíntota oblicua de f(x) <=>

n = lim_x->inf f(x) - mx

m = lim_x->inf f(x)/x

La Recta

Se define como el objeto ideal que se extiende en una misma dirección y contiene una sucesión continua e infinita de puntos en una sola dimensión, no posee principio ni fin.

En geometría analítica llamamos línea recta al lugar geométrico de los puntos tales que al tomar dos puntos diferentes cualesquiera P₁(X₁,Y₂) Y P(X₂,Y₂) del lugar, el valor de la pendiente m calculado por medio de la formula m=(Y₁-Y₂)/(X₁-X₂)

Pendiente Y Angulo de inclinación

La pendiente es el grado (medida) de inclinación de una recta, la razón de cambio en y con respecto al cambio en x. Si una recta pasa por dos puntos dintintos (x₁, y₁) y (x₂, y₂), entonces su pendiente (m) está dada por:

Donde m representa la pendiente entre el punto 1 y el punto 2. La cual representa la razón de cambio de y respecto a x, es decir si (x) se incrementa en 1 unidad, (y) se incrementa en (m) unidades.

Si la pendiente (m)es mayor que 0 se dice que la pendiente es positiva, si la pendiente es menor que 0 se dice que la pendiente es negativa, si la pendiente es igual a 0 la recta es paralela al eje (x) del plano cartesiano, y si la pendiente es indefinida la recta es paralela al eje (y) del plano cartesiano.

El ángulo θ que una recta tiene con el eje positivo de x, está relacionado con la pendiente M, en la siguiente ecuación:

     

y    

Dos o más rectas son paralelas si ambas poseen la misma pendiente, o si ambas son verticales y por ende no tienen pendiente definida; 10 o más rectas son perpendiculares (forman un ángulo recto entre ellas) si el producto de sus pendientes es igual a -1, o una posee pendiente 0 y la otra no esta definida (infinita).

Ejemplo: Encuentre la pendiente y ángulo de inclinación de la recta que pasa por los puntos A (-6,-4) y B (8,3).

así Aplicando la formula:

  

      

     se tiene m= 3-(-4)/8-(-6)=7/14= 1/2

para obtener el ángulo esto es :Tang-1 (.5)=26° 33''

Ecuaciones de la recta

PENDIENTE ORDENADA EN EL ORIGEN

Ecuación de la línea recta con pendiente y ordenada en el origen.

Sea una recta con pendiente m que intersecta al eje y en el punto (O,b), siendo b la ordenada al origen y sea P(X,Y) otro punto de la recta como se indica en la figura:

Aplicamos la fórmula de la pendiente: 

Despejando y tendremos la ecuación de la recta de pendiente-ordenada en el origen (intersección).

y = mx + b

Ejemplo:  Determina la ecuación de la recta cuya pendiente es m=2 y corta al eje de las ordenadas en el punto    (0,3), en este ejemplo debemos de considerar a b=3

aplicando la formula vista anteriormente tenemos:  y = mx + b  y con ello tenemos el resultado de: y = 2x + 3

ECUACION PUNTO PENDIENTE

Partiendo de la ecuación continua la recta Y quitando denominadores: Y despejando: Como Se obtiene: Ejemplo:  Una recta pasa por el punto A(-1, 3) y tiene un vector director = (2,5). Escribir su ecuación punto pendiente. ECUACIÓN SIMÉTRICA DE LA RECTA La ecuación canónica o segmentaria de la recta es la expresión de la recta en función de los segmentos que ésta determina sobre los ejes de coordenadas. a es la abscisa en el origen de la recta. b es la ordenada en el origen de la recta. Los valores de a y de b se se pueden obtener de la ecuación general.                                                                                              Si y = 0 resulta x = a.                                                                                              Si x = 0 resulta y = b. Una recta carece de la forma canónica en los siguientes casos:                                                                                           1.-Recta paralela a OX, que tiene de ecuación y y= n                                                                                           2.-Recta paralela a OY, que tiene de ecuación x x= k                                                                                           3.-Recta que pasa por el origen, que tiene de ecuación y = mx. Ejemplo: Una recta determina sobre los ejes coordenados, segmentos de 5 y 3 unidades, respectivamente. Hallar su ecuación.

ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS

Sean P(x1,y1) y Q(x2,y2) dos puntos de una recta. En base a estos dos puntos conocidos de una recta, es posible determinar su ecuación. Para ello tomemos un tercer punto R(x,y), también pertenciente a la recta. Como P, Q y R pertenecen a la misma recta, se tiene que PQ y PR deben tener la misma pendiente. O sea     y    Luego, la ecuación de la recta que pasa por dos puntos es: que también se puede expresar como Ejemplo: Determina la ecuación de la recta que pasa por los puntos P(1,2) y Q(3,4) y - 2 = x - 1 x - y + 1 = 0

ECUACIÓN GENERAL DE LA RECTA

Esta es una de las formas de representar la ecuación de la recta.

De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano), con abscisas (x) y ordenadas (y).

Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano.

Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación

Ax + By + C = 0

Que también puede escribirse como

ax + by + c = 0

y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:

Teorema La ecuación general de primer grado Ax + By + C = 0, donde A, B, C pertenecen a los números reales ( );  y en que A y B no son simultáneamente nulos, representa una línea recta.

Intersección de rectas

Dos recta se intersecan cuando ambas coinciden en un solo punto del plano cartesiano. Para que esto suceda, ambas rectas deben poseer diferente pendiente.

Relación entre rectas

Al comparar dos rectas en un plano estas pueden ser paralelas, perpendiculares, que haya intersección en un solo punto sin ser perpendiculares o que sean coincidentes.

RECTAS PARALELAS

Dos o mas rectas son paralelas si tienen la misma pendiente o el mismo ángulo de inclinación, las identificamos porque son rectas que jamás se cortan.

Analíticamente, las ecuaciones de las rectas paralelas poseen estas características:

Si se expresan en la forma común, son diferentes únicamente en la ordenada al origen.

Si en la forma general, tanto el signo como el coeficiente de X y Y(denotados por A y B, respectivamente) son iguales y únicamente cambian el termino independiente (C). 

RECTAS PERPENDICULARES

Dos rectas son perpendiculares si al cortarse dividen el plano en cuatro regiones iguales, cada una de las cuales forma un ángulo recto; el punto de intersección de dos rectas perpendiculares se denomina pie de una recta respecto de la otra.

RECTAS COINCIDENTES

Dos rectas son coincidentes si todos sus puntos son comunes; es decir, gráficamente son la misma recta. ¿Cómo se obtienen las rectas coincidentes?. Si conocemos la ecuación de la recta, simplemente multiplicamos ambos miembros de la ecuación por un mismo numero, sea entero o fraccionario.

RECTAS QUE SE CORTAN EN UN SOLO PUNTO

SECCIONES CONICAS

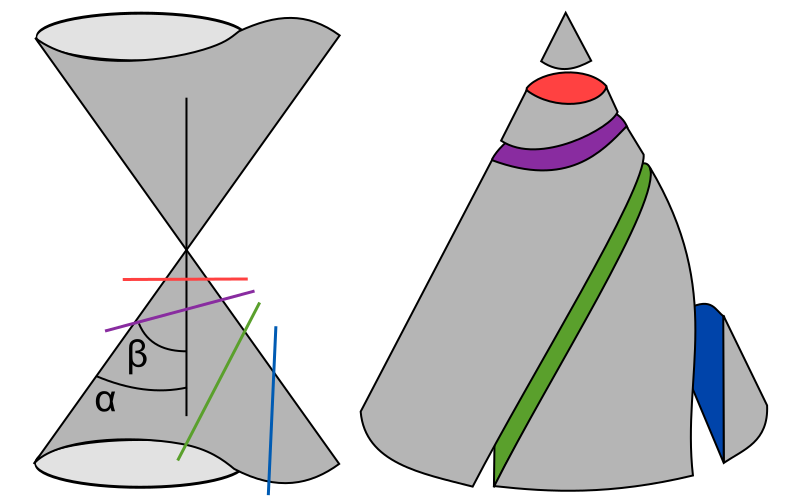
Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse, parábola e hipérbola. Un cono circular recto de dos hojas con un plano que no pasa por su vértice

De acuerdo al ángulo y el lugar de la intersección es posible obtener círculos, hipérbolas , elipses o parábolas. Cuando el plano solo toca uno de los mantos del cono y no es paralelo a una de sus aristas se obtiene una Elipse. Cuando el plano corta los dos mantos del cono se obtiene una hipérbola. Cuando el plano que corta es paralelo a una de las aristas del cono se obtiene una parábola.

 Tipos: En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:

• β < α : (naranja)
• β = α : (azulado)
• β > α : (verde)
• β = 90º:(un caso particular de elipse) (rojo)

Si el plano pasa por el vértice del cono, se puede comprobar que:

• Cuando β > α la intersección es un único punto (el vértice).
• Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
• Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
• cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).

Aplicaciones: Las curvas cónicas son importantes en astronomía: dos cuerpos masivos que interactúan según la ley de gravitación universal, sus trayectorias describen secciones cónicas si su centro de masa se considera en reposo. Si están relativamente próximas describirán elipses, si se alejan demasiado describirán hipérbolas o parábolas. También son importantes en aerodinámica y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas.

LA CIRCUNFERENCIA

La circunferencia es una línea curva, plana y cerrada, cuya definición más usual es: Una circunferencia es el conjunto de todos los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro. A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene. Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio. La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica. Elementos de la circunferencia Existen varios puntos, rectas y segmentos, singulares en la circunferencia: Centro, el punto interior equidistante de todos los puntos de la circunferencia; Radio, el segmento que une el centro con un punto cualquiera de la circunferencia; Diámetro, el mayor segmento que une dos puntos de la circunferencia (necesariamente pasa por el centro); Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros) Recta secante, la que corta a la circunferencia en dos puntos; Recta tangente, la que toca a la circunferencia en un sólo punto; Punto de tangencia, el de contacto de la recta tangente con la circunferencia; Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia; Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro. Ecuación de la circunferencia con centro en (0,0)

Cuando el centro está en el origen (0, 0), la ecuación de una circunferencia se simplifica a: A está ecuación se le conoce como ecuación canónica y se da cuando el centro de la circunferencia es el punto C(0,0), por lo que la expresión ordinaria queda reducida a:

Ecuación de la circunferencia con centro en (h,k)

En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (h, k) distinto del origen y radio r consta de todos los puntos (x, y) que satisfacen la ecuación.

(x-h)² + (y-k)² =r², donde (h,k) es el centro y r es el radio.

Para determinar la ecuación ordinaria de a circunferencia se necesita las coordenadas del centro y la medida del radio.

Ecuación general de la circunferencia

Si conocemos el centro y el radio de una circunferencia, podemos construir su ecuación ordinaria, y si operamos los cuadrados, obtenemos la forma general de la ecuación de la circunferencia, así:

Demostración:

LA PARÁBOLA

Una parábola: es el lugar geométrico de los puntos de un plano equidistantes a una recta dada, llamada directriz, y a un punto fijo que se denomina foco. El lado recto. El lado recto mide 4 veces la distancia focal, Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto y mide 4 veces la longitud de p. Elementos de la parábola La Directriz: es la recta sobre la cual si medimos su distancia hasta un punto cualquiera de la parábola, esta debe ser igual a la distancia de este mismo punto al Foco. El eje focal: es la recta perpendicular a la directriz que pasa por el foco. Vertice: Es el punto en el cual la parábola corta el eje focal. Lado Recto:  Es un segmento paralelo a la directriz, que pasa por el foco y es perpendicular al eje focal y sus extremos son puntos de la parábola (A,B). La distancia entre el vértice y la directriz que es la misma entre el vértice y el foco de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p). Los puntos de la parábola están a la misma distancia del foco F y de la recta directriz.

Ecuaciones de la parábola con vértice en el origen

Primeramente, estudiaremos la ecuación de la parábola para los casos en que su vértice esté en el origen (coordenadas (0, 0) delPlano Cartesiano), y según esto, tenemos cuatro posibilidades de ecuación y cada una es característica.

Para iniciar nuestra explicación empezaremos con la parábola cuyo vértice está en el origen, su eje focal o de simetría coincide  con el eje de las X (abscisas) y que está orientada (se abre)  hacia la derecha.

Por definición, sabemos que, en una parábola  la distancia entre un punto “P” (no confundir con el “parámetro p”),   cualquiera de coordenadas (x, y), y el foco “F”  será igual a la distancia entre la directriz (D) y dicho punto, como vemos en la figura:

De lo anterior resulta:

                                   

(trazo PD igual al trazo PF)

El trazo PD nace en el punto (x, y) y termina en el punto (–p, y) y podemos usar la fórmula para calcular distancia entre dos puntos:

                                                       

El trazo PF nace en el punto (x, y) y termina en el punto (p, 0), y también podemos usar la fórmula para calcular la distancia entre ellos:
                                                            

Sustituyendo en la expresión de distancias                                                                     resulta:

                                                          

Elevando ambos miembros de la ecuación al cuadrado y desarrollando, se tiene:

(x + p)² = (x – p)² + y²

x² + 2px + p² = x² – 2px + p² + y²

x² + 2px + p² – x² + 2px – p² = y²

Simplificando términos semejantes y reordenando la expresión, se obtiene:

y2 = 4px

que es ecuación de la parábola en su forma ordinaria o canónica.

Esta ecuación tiene leves variaciones según sea la orientación  de la parábola (hacia donde se abre).

Veamos ahora las cuatro posibilidades:

Primera posibilidad

La que ya vimos, cuando la parábola se abre hacia la derecha (sentido positivo) en el eje de las abscisas “X”

Ecuación de la parábola       y2 = 4px Ecuación de la directriz        x + p = 0

Segunda posibilidad

Cuando la parábola se abre hacia la izquierda (sentido negativo)  del eje de las abscisas “X”.

Ecuación de la parábola       y2 = –4px Ecuación de la directriz        x – p = 0

Tercera posibilidad

Cuando la parábola se abre hacia  arriba (sentido positivo) en el  eje de las ordenadas  “Y” .

Ecuación de la parábola       x2 = 4py Ecuación de la directriz        y + p = 0

Cuarta posibilidad

Cuando la parábola se abre hacia abajo (sentido negativo) en el eje de las ordenadas  “Y”.

Ecuación de la parábola       x2 = –4py Ecuación de la directriz        y – p = 0

Información importante:

El parámetro p (que marca la distancia focal)  señala  la distancia entre el foco y el vértice, que es igual a la distancia entre elvértice y la directriz.

Si en la ecuación de la parábola la incógnita x es la elevada al cuadrado, significa que la curvatura de la misma se abre hacia arriba o hacia abajo, dependiendo  del signo del parámetro  p.

Cuando el parámetro p es positivo, la parábola se abre “hacia arriba” y cuando es negativo se abre “hacia abajo”.

Ahora, si en la ecuación de la parábola la incógnita y es la elevada al cuadrado, la curvatura de la misma será hacia la derecha o hacia la izquierda. En este caso, cuando el parámetro p es positivo, la parábola se abre “hacia la derecha” y cuando es negativo se abre “hacia la izquierda”.

Longitud del lado recto (LR)

Tal como dedujimos la ecuación anterior, es posible deducir la ecuación que nos permita calcular la longitud del lado recto (cuerda que pasa por el foco, perpendicular al eje focal o de simetría):

No desarrollaremos el camino y sólo diremos, para recordar, que el lado recto es igual a 4p.

Ejemplo:

Obtener la ecuación, el foco y la directriz de la parábola con vértice en el origen y que contiene al punto B(3, 4), además su eje de simetría (o eje focal) es paralelo al eje X.

Resolución: 

El punto B (3, 4) nos indica que

X = 3

Y = 4

 Sustituyendo las coordenadas del punto B en la ecuación

Entonces la ecuación será

Y el Foco estará en el punto 4/3, 0

    

Vemos que 4/3 corresponde al valor de p, y como la directriz está a la misma distancia de p respecto al vértice, pero hacia el lado contrario, entonces, la directriz será:

             

                                 

Ecuación de la parábola cuyo vértice no está en el origen

Ahora analizaremos los casos en que se puede obtener la ecuación que describe una parábola cuyo vértice no coincide con el origen del sistema de ejes coordenados.

Cuando el vértice de la parábola se localiza en cualquier punto, por convención ubicado en las coordenadas (h, k), y distinto al origen, la ecuación que describe a la parábola cambia en función de la posición de este punto y de la orientación de apertura respecto de los ejes x e y.

Debido a estas características, también tenemos cuatro posibilidades de ecuaciones de parábolas cuyo vértice está fuera del origen del sistema de ejes coordenados.

Primera posibilidad

Que la parábola se abra hacia la derecha (sentido positivo) en el eje de las abscisas “X”.

Ecuación de la parábola    (y – k)2 =  4p(x – h) Ecuación de la directriz      x – h + p = 0

Segunda posibilidad

Que la parábola se abra hacia la izquierda (sentido negativo) del eje de las abscisas “X”.

Ecuación de la parábola           (y – k)2 = 4p(x – h) Ecuación de la directriz             x – h – p = 0

Tercera posibilidad

Que la parábola se abra hacia arriba (sentido positivo) del eje de las ordenadas “Y”

Ecuación de la parábola       (x – h)2 = 4p(y – k) Ecuación de la directriz        y – k + p = 0

Cuarta posibilidad

Que la parábola se abra hacia abajo (sentido negativo)  del eje de las ordenadas “Y”.

Ecuación de la parábola    (x – h)2 = –4p(y – k) Ecuación de la directriz     y – k – p = 0

Recuerde que en todos los casos anteriores la longitud del lado recto siempre será LR = 4p.

 Veamos unos ejemplos:

Ejemplo 1:

Encontrar la ecuación de la parábola con vértice en el punto (3, 2) y foco en (5, 2).

Desarrollo

Al analizar las coordenadas de vértice (3, 2) y foco (5, 2), vemos que su ordenada es común (y = 2), por lo que se concluye que están alineados horizontalmente y que el foco está a la derecha del vértice.

Según ya vimos, en este caso la ecuación que resulte tiene la forma

(y – k)² = 4p(x – h)

Siendo las coordenadas del vértice (h, k), se sustituyen en la ecuación y resulta:

(y – 2)² = 4p(x – 3)

En donde el parámetro p representa la distancia del vértice al foco, que podemos calcular por diferencia de las abscisas correspondientes:

p = 5 – 3

p = 2

Sustituyendo:

(y – 2)² = 4(2)(x – 3)

Queda

(y – 2)² = 8(x – 3),

ecuación escrita en la forma ordinaria o canónica.

Ecuación de la parábola en su forma general

En todos los casos, la estructura de la ecuación de la parábola tiene las siguientes características:

Existe solamente una variable al cuadrado (x² o bien y²) y otra lineal.

El coeficiente de la variable lineal (4p) (el coeficiente es el 4) representa la proporción del lado recto con respecto de la distancia focal (debemos recordar que la distancia focal es la distancia entre el foco y el vértice).

Pero además de lo anterior, desde el punto de vista de las estructuras algebraicas, la ecuación de la parábola es una ecuación de segundo grado, que puede expresarse en la forma general de ecuaciones de este tipo.

Obtención de la ecuación general de la parábola

Para llegar a dicha expresión o forma general, es necesario desarrollar  algebraicamente la forma ordinaria o canónica de la ecuación.

Tomando como ejemplo la forma:

(x – h)² = 4p(y – k)

Desarrollando resulta:

x² – 2hx + h² = 4py – 4pk

x² – 2hx + h² – 4py + 4pk = 0

Multiplicando la ecuación por un coeficiente “A” con la intención de generalizar, y considerando A ≠ 0, tendremos:

Ax² – 2Ahx + Ah² – 4Apy + 4Apk = 0

Reordenando:

Ax² – 4Apy – 2Ahx – Ah² + 4Apk = 0

Ax² – 4Apy – 2Ahx + A(h² + 4pk) = 0

Haciendo que los coeficientes de las variables sean:

–4Ap = B

–2Ah = C

A(h² + 4pk) = D

Sustituyendo los coeficientes B, C y D en la ecuación, nos queda

Ax2 + Bx + Cy + D = 0

que es la ecuación de una parábola horizontal en su forma general.

Análogamente, para una parábola de orientación vertical, la ecuación en su forma general será:

Ay2 + Bx + Cy + D = 0

Ejemplo I

Una parábola tiene vértice en el punto (–4, 2), y su directriz es y = 5, encuentre su ecuación y exprésela en la forma general.

Desarrollo

Analizando las coordenadas del vértice y la posición de la directriz, se puede concluir que:

a) La directriz es paralela al eje de las abscisas, por lo tanto la posición de la parábola es vertical.

b) La directriz corta al eje de las ordenadas en un valor (5) mayor que la ordenada del vértice (2), por lo tanto la parábola se  abre hacia abajo (sentido negativo del eje de las Y).

c) Las coordenadas del vértice no corresponden con las del origen.

d) Dado lo anterior, se trata entonces de una parábola cuya ecuación ordinaria o canónica es del tipo:

(x – h)2 = –4p (y – k)

De las coordenadas del vértice se obtiene:

h = –4

k = 2

Se obtiene p por diferencia entre las ordenadas del vértice y de la directriz, resultando:

p = 5 – 2

p = 3

Sustituyendo valores en la ecuación ordinaria, resulta:

(x – h)² = –4p(y – k)

(x – (–4))² = –4 (3) (y – (+2))

(x + 4)² = –12(y – 2)

(x + 4)² = –12y + 24

Desarrollando el binomio al cuadrado

(x + 4) (x + 4) = x² + 8x + 16

x² + 8x + 16 = +12y – 24

Simplificando e igualando a cero la ecuación se tiene:

x² + 8x + 16 + 12y – 24 = 0

x² + 8x + 12y – 8 = 0

Que es la ecuación buscada.

Calcular los parámetros de la parábola  si nos dan su ecuación general.

Reducción de la ecuación de una parábola

Dada una ecuación del tipo

Ax² + Bx + Cy + D = 0

o del tipo

Ay² + Bx + Cy + D = 0,

siempre es posible reducir la ecuación de una parábola. Para ello se completa un cuadrado y se manipula adecuadamente el otro miembro.

ELIPSE

Una elipse es el conjunto de todos los puntos P en un plano tal que la suma de las distancias desde P a dos puntos fijos es una constante dada. Cada uno de los puntos fijos es llamado un foco. (El plural es focos.)

Los segmentos  PF1 y PF2 son los radios focales de P.

El centro de la elipse es el punto medio del segmento de línea que une sus focos. El eje mayor de la elipse es la cuerda que pasa a través de sus focos y tiene sus puntos finales en la elipse. El eje menor de la elipse es la cuerda que contiene el centro de la elipse, tiene sus puntos finales en la elipse y es perpendicular al eje mayor.

         

         Una elipse tiene una ecuación cuadrática con dos variables. 

         Dada una elipse con su centro en (0, 0), sus focos en el eje de las x en (c, 0) y (–c, 0), las intercepciones enx (±a, 0) y las intercepciones en y en (0, ±b). La suma de sus radios focales es 2a y su ecuación es

          

         El eje mayor está en el eje de las x.

         

         Si los focos en la elipse están en el eje de las y, entonces los puntos focales son (0, ±c), y la fórmula es

          

         El eje mayor está en el eje de las y. Las intercepciones en x son (±b, 0) y las intercepciones en y son (0, ±a).

         

Dese cuenta que el eje mayor es horizontal si el término x² tiene el denominador más grande y vertical si el término y² tiene el denominador más grande. Ya que el más grande de los dos denominadores es a², la longitud del eje mayor siempre es 2a y la longitud del eje menor siempre es 2b. La distancia del centro a cualquier foco es |c|.

Ya que el centro de cada una de estas elipses tienen su centro en el origen, son llamadas elipses centrales.

          

EVALUACION

GEOMETRIA ANALITICA

1.-¿SE LE CONOCE COMO EL PADRE DE LA GEOMETRIA ANALITICA?

A) APOLONIO

B) RENE DESCARTES

C) GAUSS

D)ARISTOTELES

2.- ¿SON LOS TRES SISTEMAS DE COORDENADAS RECTANGULAES?

A) UNIBIDIMENSIONAL,2D, TRIDIMENSIONAL

B) UNA DIMESION, 2D, 3D

C) UNIDIMENSIONAL, BIDIMENSIONAL, TRIDIMENSIONAL

D) UNIDIMENSIONAL, BIDIMENSIONAL, TERCERA DIMENSION

3.- ¿SEGMENTO D ERECA QUE TIENE DIRECCION?

A) SEGMENTO DIRIGIDO

B) LINEA RECTA

C) SEGMENTO

D) TRAMO

4.- ¿EXPRESA LA PROXIMIDAD Y LEJANIA ENTRE DOS PUNTOS?

A)LONGITUD

B)PERIMETRO

C)DISTANCIA

D)AREA

5.- ¿ CALCULA DISTANCIA ENTRE LOS PUNTOS C(5,-3) Y D5,6)?

A) 3

B)9

C)3³

D)9/2

6.-  SI EL SEGMENTO AB SE DIVIDE EN TRES PARTE IGUALES LA RAZÓN PARA P1 ES:

A)1/4

B) 3

C)2

D)1/2

7.- EN UN SISTEMA DE COORDENAS POLARES SU ORIGEN SE ENCUENTRA EN

A) 0,0

B) 0°,0

C) 0,0°

D) 0,2∏

8.- ¿SE DETERMINA POR LA LETRA GRIEGA Ө?

A) ANGULO

B) RADIO

C) ANGULO POLAR

D) POLO

9.-TRANSFORMA LAS COORDENADS DEL PUNTO P(6,30°) A COORDENADAS RECTANGULARES

A)3, 30°

B) 3, 6

C)3,3

D) 3, 3

10.-¿LOS 360° ENQUIVALEN A CUANTOS RADIANES?

A) ∏ RADIAN

B) 2∏ RADIANES

C) 1/4∏ RADIANES

D) 90∏ RADIANES

11.- CALCULA EL AREA DEL RECTANGULO

A)192

B)28

C) 140

D)96

12.- CUAL DE LAS SIGUIENTES ECUACIONES PERTENECEN A LA RECTA

A) PUNTO PENDIENTE, GENREAL Y SIMETRIA

B) SIMETRIA, ORDENADA AL ORIGEN Y CANONICA

C) CANONICA, SIMETRIA Y PUNTO PENDIENTE

D) PUNTO PENDIENTE, ORDENA AL ORIGEN Y ECU. GENERAL

13.- DETERMINA LA ECUACIÓN DE LA RECTA CUYA PENDIENTE ES M=2 Y CORTA AL EJE DE LAS ORDENADAS EN EL PUNTO    (0,3), EN ESTE EJEMPLO DEBEMOS DE CONSIDERAR A B=3.

A)  y = 2x + 3

B) y = 4x + 3

C) y = 2x + 6

D) y = 4x + 6

14.- DETERMINA LA ECUACIÓN DE LA RECTA QUE PASA POR LOS PUNTOS P(1,2) Y Q(3,4).

A)  2x - y + 1 = 0

B)  x - 2y + 1 = 0

C) x - y + 1 = 0

D) x - y + 1 = 2

15.- SI LA RECTA CON PENDIENTE IGUAL A 2 PASA POR EL PUNTO (0,2) Y LA RECTA 2 PASA POR EL PUNTO (0.8) CON UNA PENDIENTE DE -3. ENCUENTRA LAS COORDENAS DEL PUNTO DE INTERSECCCION.

A) 2, 4

B) 4, 2

C) 4, 4

D) 2,2

16.- ¿ CUAL DE LOS SIGUIENTES PARES DE ECUCIONES CORRESPONDEN A UNAS RECTAS QUE SON PARALELAS?

A) x -y + 1 = 0, x - 2y + 1 = 0

B) 2x - 2y + 1 = 0, x - 2y + 1 = 0

C)  4x - y + 1 = 0, 4x - 2y + 6 = 0

D) x - 2y + 1 = 0, 4x - 2y + 1 = 0

17.-¿ SON SECCIONES CONICAS?

A) CIRCULO, TRIANGULO, ELIPSE

B) CIRCUNFERENCIA, ELIPSE, PARABOLA

C) PARABOLA, CUADRADO, TRIANGULO

D) CIRCUNFERENCIA, ELIPSE, ROMBO

18.- ¿ SON ELEMNTOS DE LA CIRCUNFERENCIA?

A) ANGULO, RADIO, CENTRO

B) RADIO, CENTRO, DIAMETRO

C) PERIMETRO, RADIO, CENTRO

D) ANGULO, PERIMETRO, CENTRO

19.- DETERN¿MINA LA ECUACION DE LA CIRCUNFERENCIA SI PASA POR EL PUNTO P(4,4) Y TIENE CENTRO EN EL ORIGEN

A) 16 + 4= 4²

B) 4²+ 4²= 4²

C) 2² + 16 = 16

D) 4² +4²= 2

20.-  UNA CIRCUNFERENCIA TIENE CENTRO EN EL PUNTO C(-4,1) Y SU RADIO ES IGUAL A 3. CON BASE EN ESTOS DATOS DETERMINA SU ECUACION.

A) (X+4)² + (Y-1)² =9

B) (X+4²)² + (Y-1²)² =9

C) (X+4)² + (Y-1)² =9²

D) (X²+4) + (Y²-1) =9

Respuestas

1.- B) , 2.- C), 3.- A), 4.- C), 5.- B), 6.- D), 7.- C), 8.- C), 9.- D), 10.- B), 11.- D), 12.- D), 13.- A), 14.- C) , 15.- D), 16.- C), 17.- B), 18.- B), 19.- B), 20.- C)